[패스트캠퍼스] 김기현의 딥러닝을 활용한 자연어처리 입문 올인원 패키지
Part 1. 딥러닝 초급
Ch 04. Geometric Perspective - 01. 차원의 저주
Ch 04. Geometric Perspective - 03. 매니폴드(Manifold) 가설
Ch 04. Geometric Perspective - 05. 정리하며
강의를 듣고 작성하였습니다.
Curse of Dimensionality(차원의 저주)
차원이 높아짐에 따라 데이터가 희소하게 분포하게 되는 문제가 발생한다.
여기서 데이터가 희소하게 분포하는 것이 무엇인지에 대해 그동안 정확히 이해하지 못한채로 넘어갔었는데, 김기현 선생님께서 명확하게 설명해주셨다.
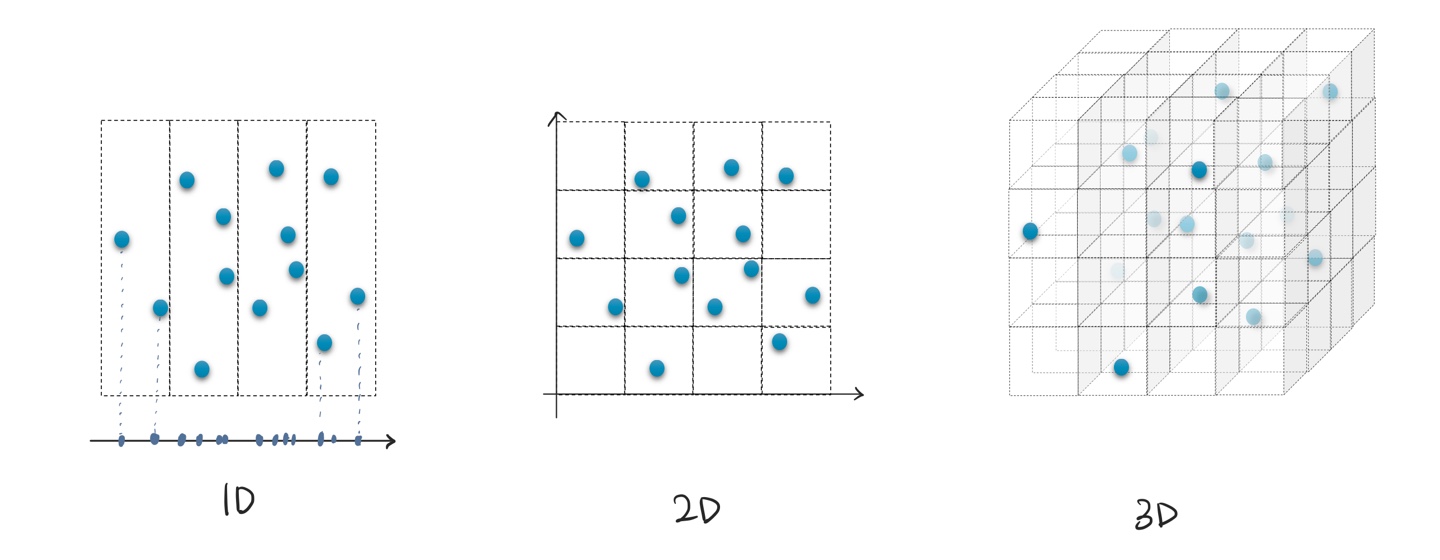
위의 그림처럼 1D에 데이터가 분포한다고 하면 4칸만 확인하면 데이터 분포를 확인할 수 있다. (1차원에 데이터가 존재한다는 것은 저렇게 직선 위에 데이터가 위치하는 것을 의미한다.)
2D의 경우에는 4x4($4^2$) 칸을 모두 확인해야 데이터를 확인할 수 있다.
3D의 경우에는 맨 오른쪽 정육면체처럼 $4^3$개의 공간을 모두 살펴봐야한다. 하지만, 점이 안찍혀있는 빈 공간도 적은 차원일 때보다 많아졌다. 즉, 모든 구역을 살펴보는게 의미가 없다는 뜻이다. 이렇게 빈 공간이 많다는 것이 데이터가 희소하게 분포한다는 뜻이다.
차원이 높을수록 데이터는 희소하게 분포하여 학습이 어려워진다. (모든 점들을 학습하기 위해서 모든 구역들을 살펴보아야 하기 때문에)
= 희소성이 높을수록 모델링 난이도가 높아진다.
그러므로 데이터의 특징(feature)을 더럽히지 않으면서 낮은 차원에서 표현해야 한다.
Manifold Hypothesis
딥러닝에서의 차원축소에서 근본이 되는 가설
고차원 공간의 샘플들이 저차원 다양체(manifold)의 형태로 분포해 있다는 가정
샘플들이 모두 균일하게 존재하는 것이 아니고 한 공간에 뭉쳐있을 확률이 높다.
쓸데없는 차원을 날려버리면 더 낮은 차원의 공간에 데이터를 위치시킬 수 있을 것이다.
ex) 3차원 공간에 2차원 형태로 데이터가 존재할 수 있다.

예를 들면, 왼쪽 그림과 같이 고차원 공간에 데이터가 저렇게 존재한다고 하자. 이는 데이터가 모든 공간에 균등하게 퍼져있는 것이 아니라 저렇게 말려있는 형태로 데이터가 분포한다고 하자. (빈 공간이 있는 것)
이렇게 비어있는 공간이 많고 모든 데이터가 균일하게 분포한게 아니므로 저차원 공간에 말린 것을 펴서 표현할 수 있을 것이다. (실제로 고차원에 데이터가 분포한다고 했지만 사실은 저차원 형태로 존재하는 것)
= 이 manifold를 해당 차원의 공간에 mapping 할 수 있다
이때 고차원 공간에서의 두 점 사이의 거리는 저차원 공간으로의 맵핑 후 거리가 다르다. 하지만 저차원 공간으로 맵핑해서 거리를 재는 것이 더 의미가 있다.
고차원 공간에서 왼쪽 그림과 같이 두 점 사이의 거리(최단거리)를 잰다면, 검은색 화살표(↔) 사이를 나타낼 것이다. 하지만 그 직선 사이에는 데이터가 존재하지 않으므로 이 거리는 의미가 없다.
하지만 저차원 공간에 맵핑한 후 거리를 재면 그 사이에 데이터들이 있기 때문에 의미가 있는 것이다.
MNIST 숫자 데이터로 예를 들어 설명해주셨다. 고차원 공간에 존재했던 MNIST 데이터를 2차원에 맵핑하였다.
MNIST 숫자 데이터가 784(28x28)차원의 벡터라고 하자 (이는 1D 벡터로 표현된다고 해서 1D 차원에 있는 것이 아니다. 784개의 숫자로 표현되어있기 때문에 784차원의 공간에 존재한다고 볼 수 있다. 우리는 이 784차원을 상상조차 하지 못한다.)
아래 그림은 원래 784차원에 존재하는 데이터를 2차원으로 인코딩한 것을 나타낸 것이다. 3과 6을 2차원으로 인코딩하고 그 값의 평균을 구하면 0에 해당하는 값이 나오는데 이는 3과 6 사이에 0이 위치한다는 것으로 해석할 수 있다.

결론
데이터는 저차원의 manifold에 분포하고 있으며, 여기에 약간의 노이즈가 추가 되어있다.
따라서 해당 manifold를 배울 수 있다면, 더 낮은 차원으로 효율적인 맵핑이 가능하다. (Non-linear dimension reduction)
낮은 차원으로의 표현을 통해 차원의 저주를 벗어나 효과적인 학습이 가능하게 된다.
'Deep Learning > 딥러닝 기초' 카테고리의 다른 글
| [패캠] Autoencoders (0) | 2021.12.14 |
|---|---|
| [Hands-on-ml-2] 모델 평가 (0) | 2020.07.30 |
| [hands-on-ml-2] 범주형 데이터 다루기 (0) | 2020.07.25 |
| [모두를 위한 머신러닝/딥러닝] ML (0) | 2020.07.09 |
댓글