[딥러닝 모델 경량화] 다양한 종류의 Convolution
요즘 효율적인 합성곱을 이용하여 모델을 경량화시키는 부분을 공부하고 있습니다.
Xception 논문을 읽는데 이런 모르는 개념들이 있어서 찾아보게 되었습니다.
Xception, MobileNet, ShuffleNet 등 다양한 모델들에 사용되는 다양한 convolution들을 정리해보겠습니다.
(김동이 님의 발표와 환'하나'의 Deep learning! 블로그를 통해 주로 공부하였습니다.)
살펴볼 convolution들은 다음과 같습니다.
º Normal Convolution
º Grouped Convolution
º Point-wise Convolution
º Depth-wise Convolution
º Depthwise separable Convolution
먼저 몇가지 기호를 정의하도록 하겠습니다.
º W: input의 width
º H: input의 height
º C: input의 channel
º K: kernel(filter)의 크기 (즉, filter는 (K, K)가 된다.)
º M: output의 channel (filter 개수)
bias는 없다고 가정하겠습니다.
1. Normal Convolution

일반적으로 사용되는 convolution입니다.
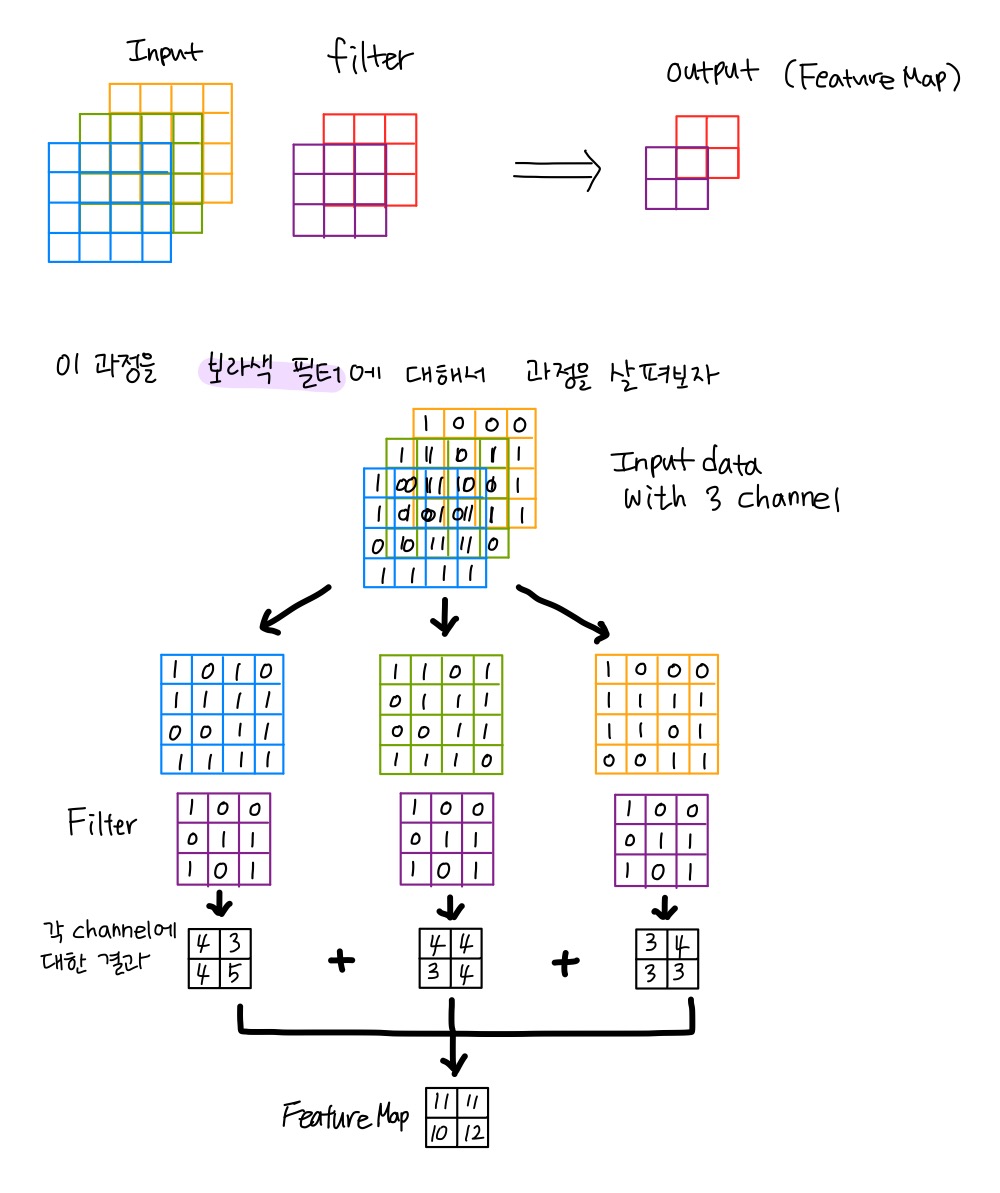
다음과 같이 예를 들어서 설명하도록 하겠습니다.
Input data의 크기가 (4,4,3)에 2x2 Filter 두 개인 convolution이라고 합시다.
Input: (4,4,3)
Filter: (2,2), 2개
Feature Map이 연산되는 과정은 다음 그림과 같이 설명할 수 있습니다.
파라미터의 수
먼저 위와 같이 한 필터에 대해 input의 각 channel을 필터와 합성곱 해주기 때문에 필터 크기와 input의 channel 개수를 곱해줍니다. $CK^2$ 가 됩니다. output을 M개의 channel로 만들어주려면 이러한 filter의 개수가 총 M개가 있어야 합니다.
따라서 input channel과 필터의 크기와 필터의 개수를 곱해준 $CK^2M$이 파라미터의 수입니다.
연산량
하나의 필터당 필요한 연산의 수를 알아내면 연산량이 구해집니다.
연산량은 $CK^2MHW$가 됩니다.
따라서 input의 크기뿐만 아니라 많은 요소들 (입력 채널의 수, 필터의 수, 커널의 크기)에 의해 연산량과 파라미터 수가 증가한다는 것을 알 수 있습니다.
2. Grouped Convolution
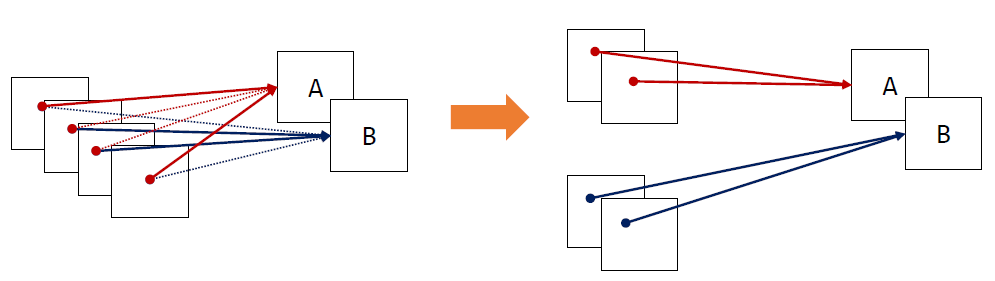
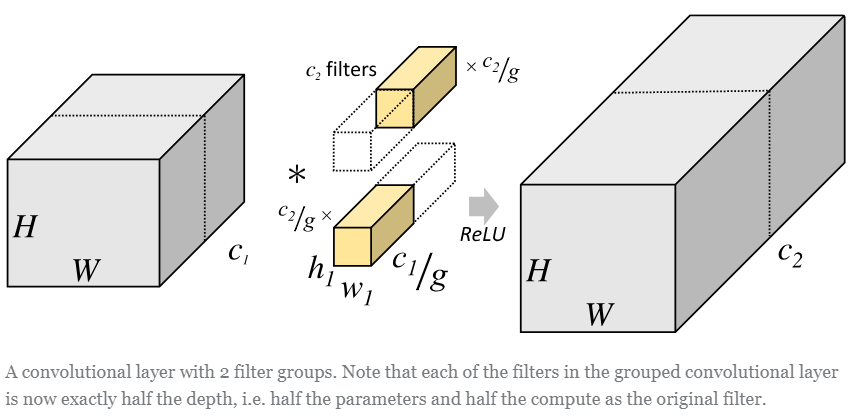
input channel을 여러 개의 그룹으로 나누어 각 그룹에 대해 독립적인 convolution을 수행하는 방식입니다.
그림4와 같이 각 그룹의 입력 채널들 사이에 독립적인 필터를 학습합니다.
grouped convolution의 장점은 다음과 같습니다.
1. 병렬 처리에 유리합니다.
2. 더 낮은 파라미터 수와 연산량을 가집니다.
3. 각 그룹에 높은 Correlation을 가지는 채널들이 학습될 수 있습니다.
파라미터의 수
각 input channel을 g개의 그룹으로 나누기 때문에 각 그룹당 channel의 수는 C/g가 됩니다. 그리고 filter도 그룹의 개수만큼 나눠서 각 그룹의 입력 채널들 사이에 나눠진 필터를 각각 독립적으로 학습시킵니다. 그래서 필터의 개수는 M/g개가 됩니다. 따라서 input channel과 필터의 크기와 필터의 개수를 곱해준 $K^2{C \over g}{M \over g}$가 각 그룹당 파라미터 수입니다.
그룹이 총 g개가 있으므로 파라미터수는 $K^2CM \over g$ 가 됩니다.
연산량
연산량은 $CK^2MHW \over g$가 됩니다.
standard convolution($CK^2MHW$)의 1/g 연산량을 가지고 있습니다.
그러나 Grouped convolution은 단점도 가지고 있습니다.
1. 그룹의 수는 Hyper parameter입니다. (그룹 수에 따라서 성능이 변화합니다.)
2. 과도하게 그룹을 나누면 각 레이어가 충분한 수의 채널을 입력으로 가질 수 없게 됩니다.
≫ 앙상블 학습과 별 차이가 없어집니다. 이는 비슷한 네트워크를 앙상블 하는 것과 같은 효과를 가진다고 보면 됩니다.
3. Depth-wise Convolution
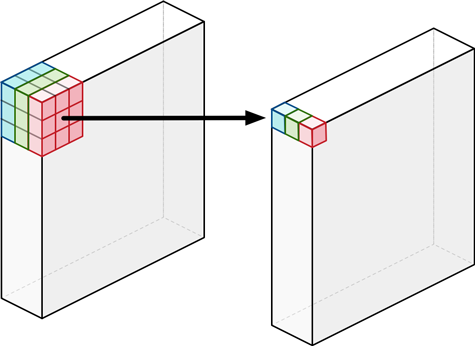
채널마다 따로 필터를 학습하는 것입니다.
일반적인 convolution filter는 입력의 모든 채널의 영향을 받게 되므로 완벽히 특정 채널만의 Spatial feature를 추출하는 것이 불가능합니다.
Depth-wise convolution은 각 단일 채널에 대해서만 수행되는 필터들을 사용합니다. 그렇기에 필터 수는 입력 채널의 수와 동일합니다.
결과적으로 입력 채널 수만큼 그룹을 나눈 Grouped Convolution과 같습니다.
파라미터의 수
각 input channel을 C개의 그룹으로 나누기 때문에 각 그룹당 channel의 수는 C/C=1가 됩니다. 그리고 filter의 수는 input channel의 수와 같기 때문에 C개입니다. 파라미터수는 $K^2C$ 가 됩니다.
연산량
연산량은 $CK^2HW$가 됩니다.
4. Point-wise Convolution (1 x 1 convolution)
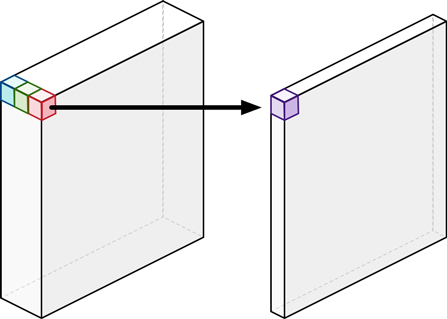
Point-wise convolution은 커널 크기(filter크기)가 1x1로 고정된 convolution layer를 말합니다.
input에 대한 Spatial Feature는 추출하지 않은 상태로, 각 채널에 대한 연산만 수행합니다. 따라서 output의 크기는 변하지 않고, channel의 수는 자유롭게 조절할 수 있습니다.
하나의 필터는 각 입력 채널별로 하나의 가중치만을 가집니다. 이 가중치는 해당 채널의 모든 영역에 동일하게 적용됩니다. 즉, 입력 채널들에 대한 Linear Combination과 같습니다.
보통 dimensional reduction을 위해 많이 쓰입니다. 이것은 channel의 수를 줄이는 것을 의미하는데 연산량을 많이 줄여줄 수 있어 중요한 역할을 하게 됩니다.
파라미터의 수
standard convoluton에서 K=1인 경우와 같습니다.
따라서 총파라미터의 수는 $CM$이 됩니다.
연산량
K=1인 경우이기 때문에 $CMHW$가 됩니다.
5. Depth-wise Separable Convolution
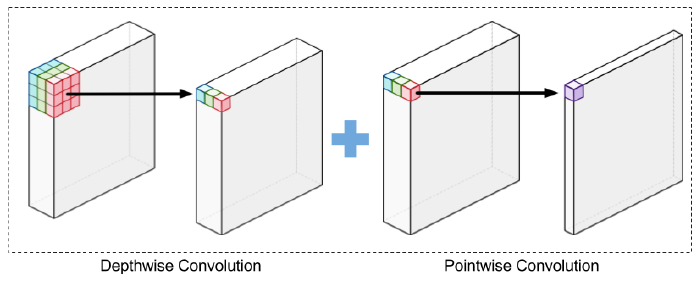
Depth-wise Convolution과 Point-wise Convolution을 조합해 사용하는 방식입니다.
기존의 Convolution에서 전체의 channel 방향과 spatial 한 방향 모두를 한꺼번에 고려했다면, 이방식은 Xception에서 제안한 방법으로, 그 둘을 완전히 분리하겠다는 아이디어입니다.
이렇게 두 방법으로 분리를 하게 되어도 channel과 spatial한 방향 모두 보기 때문에, 기존의 convolution과 유사하게 동작하지만 파라미터의 수와 연산량은 훨씬 적습니다.
각 Channel 별 Spatial Convolution을 한 이후에 Feature별 Linear combination을 해주는 것이라고 보면 됩니다.
파라미터의 수
단순히 Depth-wise convolution 후에 Point-wise Convolution을 수행하는 방식이므로 두 방식의 파라미터를 더해주기만 하면 됩니다. 따라서 총 파라미터의 수는 $K^2C+CM=C(K^2+M)$이 됩니다.
연산량
이 또한 두 방식의 연산량을 더해주기만 하면 됩니다.
$K^2CHW+CMHW=CHW(K^2+M)$
이렇게 다섯 가지의 Convolution을 정리해봤습니다.
다음에는 이 Convolution들이 사용되는 모델들에 대해서 알아보도록 하겠습니다!
출처:
[1] https://www.youtube.com/watch?v=ijvZsH4TlZc
[2] http://taewan.kim/post/cnn/
[3] https://zzsza.github.io/data/2018/02/23/introduction-convolution/
[4] https://hichoe95.tistory.com/48?category=783893
[5] https://newsight.tistory.com/310
[6] http://machinethink.net/blog/googles-mobile-net-architecture-on-iphone/
'Deep Learning' 카테고리의 다른 글
| [딥러닝 모델 경량화] Xception (0) | 2020.08.02 |
|---|---|
| [딥러닝 모델 경량화] Inception (0) | 2020.08.02 |
| [딥러닝 모델 경량화] 딥러닝 경량화 기술 동향 (1) | 2020.08.01 |
| [Hands-on-ml-2] 모델 평가 (0) | 2020.07.30 |
| [hands-on-ml-2] 범주형 데이터 다루기 (0) | 2020.07.25 |
댓글